ENUNCIADO E PROPOSTA DE RESOLUÇÃO
1. Determine as projeções do ponto I, resultante da intersecção da reta h com o plano de rampa δ.
Dados
− o plano δ contém o ponto A (0; 2; 9) e define um diedro de 60º com o Plano Horizontal de Projeção;
− o traço horizontal do plano tem afastamento negativo;
− a reta h é horizontal e contém o ponto M, do plano bissector dos diedros pares, β24, com zero de abcissa
e 5 de afastamento;
− a reta h define um ângulo de 60º, de abertura para a esquerda, com o Plano Frontal de Projeção.
2. Determine as projeções de um retângulo [ABCD] contido num plano oblíquo α.
Dados
− a diagonal [AC] mede 9 cm e pertence a uma reta do plano bissector dos diedros ímpares, β13, que
intersecta o eixo x num ponto com − 3 de abcissa;
− o vértice A tem 1 de abcissa e 3 de cota;
− o traço frontal do plano define um ângulo de 60º, de abertura para a esquerda, com o eixo x;
− o lado [AB] é frontal
3. Determine as projeções dos pontos X e Y, comuns à reta r e à superfície de um cone oblíquo de base
circular, contida num plano horizontal.
Destaque, a traço mais forte, as projeções da reta e do sólido.
Identifique, a traço interrompido, as invisibilidades do sólido e das projeções da reta.
Dados
− o ponto O (7; 8; 8) é o centro da circunferência, com 5 cm de raio, que delimita a base do cone;
− o vértice V tem zero de abcissa e pertence ao eixo x;
− o traço horizontal da reta r tem 2 de abcissa e 5 de afastamento;
− a projeção horizontal da reta r define um ângulo de 45º, de abertura para a direita, com o eixo x;
− a projeção frontal da reta r define um ângulo de 70º, de abertura para a esquerda, com o eixo x.
4. Determine as projeções de uma pirâmide oblíqua de base quadrada [ABCD], contida num plano horizontal, e das suas sombras, própria e projetada nos planos de projeção.
Destaque, a traço mais forte, as projeções do sólido e o contorno da sombra projetada nos planos de
projeção.
Identifique, a traço interrompido, as invisibilidades do sólido e do contorno da sombra projetada.
Preencha, com tracejado ou com uma mancha de grafite clara e uniforme, as áreas visíveis das sombras,
própria e projetada.
Nota – Se optar pelo tracejado, deverá fazê-lo com linhas paralelas ao eixo x, nas áreas de sombra própria, e com linhas perpendiculares às respetivas projeções da direção luminosa, nas áreas de sombra projetada.
Dados
− a aresta [AV] é de perfil e define um ângulo de 75º com o Plano Horizontal de Projeção;
− o vértice V tem zero de abcissa, 4 de afastamento e 2 de cota, e o vértice A tem 2 de afastamento;
− o vértice D tem 6 de abcissa e pertence ao Plano Frontal de Projeção;
− a direção luminosa é a convencional.
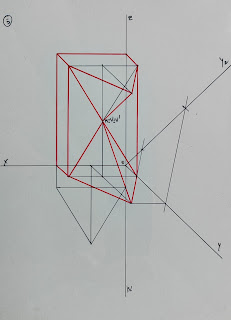
5. Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por um prisma reto de bases regulares pentagonais e uma pirâmide oblíqua de base quadrada.
Destaque, no desenho final, apenas as linhas visíveis do sólido resultante.
Dados
Sistema axonométrico:
− a projeção axonométrica do eixo y define um ângulo de 130º com a projeção axonométrica do eixo x e
um ângulo de 140º com a projeção axonométrica do eixo z;
− a inclinação das retas projetantes com o plano axonométrico é de 55º.
Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.
Prisma:
− as bases do prisma são paralelas ao plano coordenado xz;
− o ponto M (7; 4; 5) é o centro da circunferência, tangente ao plano coordenado xy, que circunscreve o
pentágono da base de maior afastamento;
− o vértice A da base de maior afastamento pertence ao plano coordenado xy;
− o prisma tem 2 cm de altura.
Pirâmide:
− as arestas da base são paralelas aos eixos coordenados x e y;
− a aresta de menor afastamento da base da pirâmide é comum à aresta, paralela ao eixo x, da base de
maior afastamento do prisma;
− o vértice V da pirâmide coincide com o vértice A do prisma.
Boas Férias 2025.