TESTE SUMATIVO Nº 2 DE 12.12.2011

Enunciado e proposta de resolução:

1.       Determine as projeções da reta s perpendicular à reta r.

Dados:

– a reta r é definida pelo ponto A(0;11;7) e pelo seu traço frontal F com 7 cm de abcissa e 2 de cota;

– a reta s, concorrente com a reta r, contém o ponto P(0;5;2).

2.       Determine as projeções e a verdadeira grandeza (V.G.) da distância do ponto P ao plano α .

Dados:

– o plano α contém as retas h e f concorrentes no ponto A;

– o ponto A tem 2 cm de afastamento e 3 cm de cota;

– a reta h é horizontal e forma, com o plano frontal de projeção, um ângulo de 45⁰, de abertura para a direita;

– a reta f é frontal e forma, com o plano horizontal de projeção, um ângulo de 30⁰, de abertura para a esquerda;

– o ponto P tem 3 cm de afastamento e 5 cm de cota, e a sua linha de chamada coincide com a linha de chamada do traço horizontal de reta f.

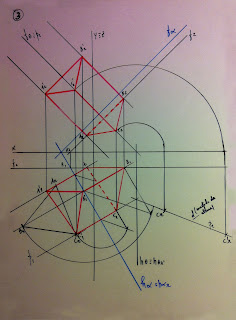
3.       Desenhe as projeções de um prisma triangular regular situado no1º diedro e com as bases contidas em planos oblíquos.

Dados:

– uma das bases do prisma é o triângulo [ABC], contido no plano α que interseta o eixo x num ponto com 3 cm de abcissa;

– os traços horizontal e frontal do plano α fazem, respetivamente, ângulos de 60⁰ (a.d.) e 45⁰ (a.d.) com o eixo x;

– o lado [AB] do triângulo é frontal e tem 1,5 cm de afastamento;

– o vértice A pertence ao β_1/3 e o vértice B tem 5 cm de cota;

– a altura do prisma mede 6 cm.

4.       Determine as projeções do ponto I de interseção da reta de perfil r com o plano de rampa ρ.

Dados:

– o plano ρ tem o seu traço horizontal com -7 de afastamento e o seu traço frontal com 4 de cota;

        – a reta r contém o ponto P(2;6;3) e é paralela ao plano bissetor dos diedros pares (β_2/4).