EXAME NACIONAL - 2ª FASE - 2013

Enunciado e proposta de resolução:

1.   Determine as projeções da reta passante s, perpendicular à reta r no ponto A.

Dados

– a reta r é passante e está definida pelo ponto A com 2 de abcissa e 3 de cota e pelo ponto  do eixo x com 7 de abcissa;

– a projeção horizontal da reta r faz um ângulo  de 50°, de abertura para a direita, com o eixo x.

Método 1

Método 2

2.   Determine, graficamente, a amplitude do ângulo formado pelos planos δ e θ.

Dados

– o plano δ é vertical, contém o ponto M do eixo x com –3 de abcissa e faz um ângulo de 60°, de abertura para a direita, com o Plano Frontal de Projeção;

– o plano θ é de topo, contém o ponto N do eixo x com 3 de abcissa e faz um ângulo de 60°, de abertura para a esquerda, com o Plano Horizontal de Projeção.

3.   Determine a sombra própria e a sombra projetada nos planos de projeção de um cilindro oblíquo, de bases circulares situadas em planos frontais, e situado no 1.º diedro.

Destaque, a traço mais forte, as projeções do cilindro e o contorno da sua sombra projetada nos planos de projeção.

Identifique, a traço interrompido, as linhas invisíveis, quer no sólido, quer na parte ocultada do contorno da sua sombra projetada nos planos de projeção.

Identifique as áreas visíveis das sombras, própria e projetada, preenchendo-as a tracejado ou com uma mancha de grafite clara e uniforme.

Nota – Se optar pelo tracejado, deverá fazê-lo com linhas paralelas ao eixo x, nas áreas de sombra própria, e com linhas perpendiculares às projeções da direção luminosa, nas áreas de sombra projetada.

Dados

– o ponto O (0; 4; 7,5) é o centro da circunferência com 3,5 cm de raio de uma das bases do cilindro;

– as geratrizes do cilindro são horizontais e fazem um ângulo de 60°, de abertura para a direita, com o Plano Frontal de Projeção;

– a outra base do cilindro pertence ao Plano Frontal de Projeção;

– a direção luminosa é a convencional.

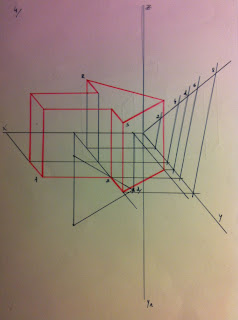
4.   Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por dois prismas   regulares.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– a projeção axonométrica do eixo y faz um ângulo de 140° com a projeção do eixo z e um ângulo de 130° com o eixo x;

– a inclinação das retas projetantes com o plano axonométrico é de 50°.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x orientado positivamente, da direita para a esquerda.

Prisma quadrangular:

– as bases do prisma pertencem a planos frontais;

– o ponto A (12; 6; 0) e o ponto B (6; 6; 0) são os vértices da aresta de menor cota da base de maior afastamento do prisma;

– o prisma tem 2 cm de altura.

Prisma triangular:

– o ponto R (6; 2; 6) e o ponto S (6; 8; 6) são os vértices da aresta de maior abcissa da base de maior cota do prisma;

– a outra base do prisma pertence ao plano coordenado xy.