1.
Determine
as projeções de um pentágono regular [ABCDE] situado num plano de rampa θ.
Dados
– o pentágono está inscrito numa circunferência com centro no ponto O
(0; 2; 5);
– a reta de perfil p do plano θ contém o ponto O e
tem o seu traço horizontal com 5 de afastamento;
– o vértice A do pentágono é o traço frontal da reta p.
2.
Determine,
graficamente, a amplitude do ângulo formado pelas retas p e f,
concorrentes no ponto B.
Dados
– a reta p de perfil é definida pelo ponto A (2; 4; 2) e
pelo ponto B com 2 de afastamento e 5 de cota;
– a reta f é frontal e faz um ângulo de 45°, de abertura para a
direita, com o Plano Horizontal de Projeção.
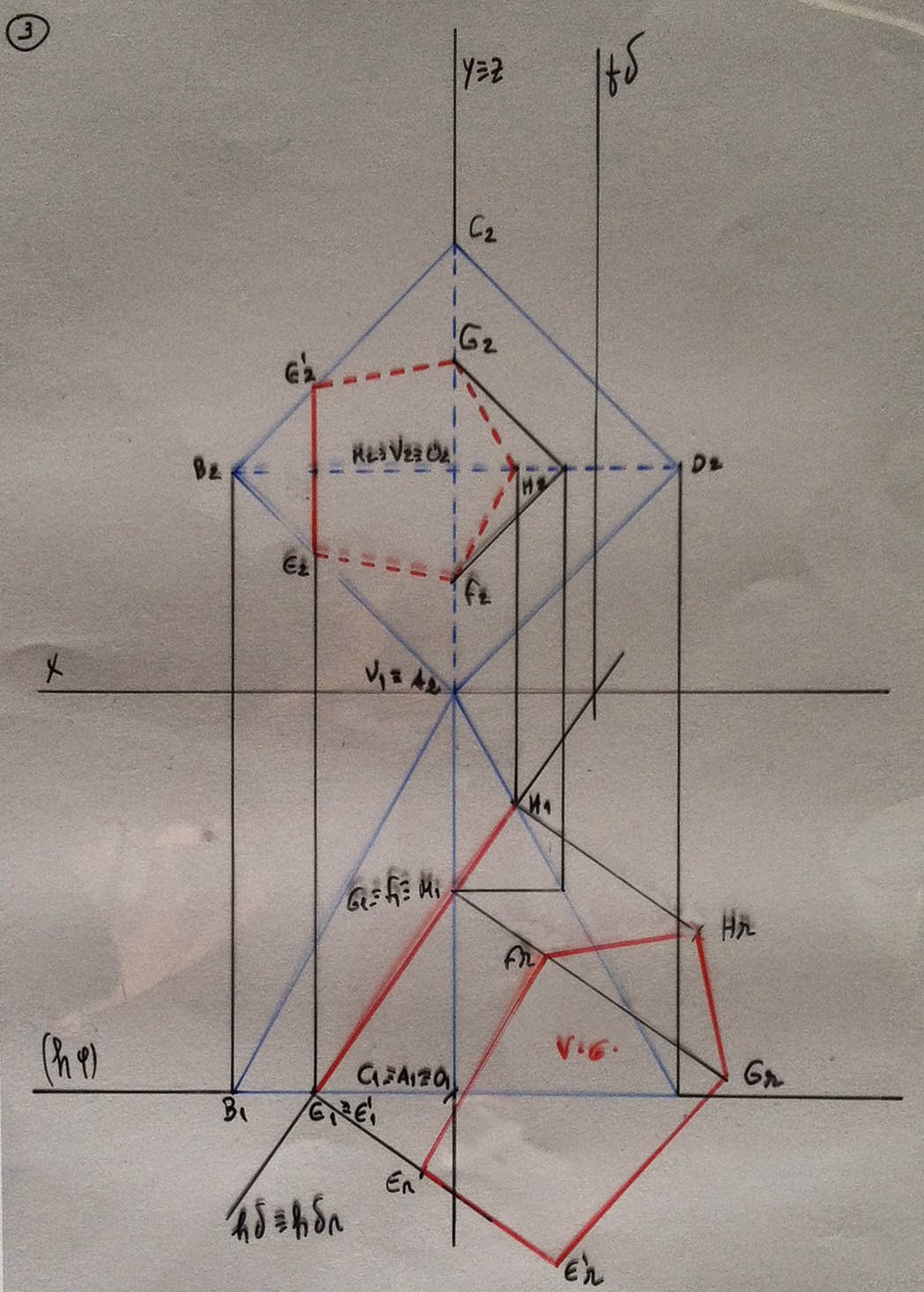
3.
Determine
as projeções e a verdadeira grandeza (V.G.) da figura da secção produzida por
um plano vertical δ numa pirâmide regular de base quadrangular [ABCD]
situada num plano frontal.
Identifique,
a traço interrompido, as arestas invisíveis do sólido resultante.
Dados
– o vértice A (0; 9; 0) é o de
menor cota;
– a diagonal [AC] do quadrado
da base é vertical e mede 10 cm;
– o vértice V do sólido
pertence ao Plano Frontal de Projeção;
– o plano δ contém o ponto M,
ponto médio do eixo do sólido, e faz um diedro de 55°, de abertura para a esquerda,
com o Plano Frontal de Projeção.
4.
Desenhe
as projeções de um prisma pentagonal
oblíquo situado no 1º diedro.
Dados:
– uma das bases do prisma é o pentágono regular [ABCDE]
contido no plano frontal de projeção;
– o centro dessa base é o ponto O(4;0;4) e o
vértice A tem 4 cm de abcissa e 7 cm de cota;
– as arestas laterais do prisma são horizontais e
fazem ângulos de 600 (a.d.) com o Plano Frontal de Projeção;
– a altura do prisma mede 5,5 cm.
Determine
as projeções do sólido resultante da secção produzida no
prisma pelo plano oblíquo α cujos traços, horizontal e frontal,
fazem ângulos de 250 (a.e.) e 550 (a.e.) com o eixo x
e são concorrentes num ponto com –6,5 cm de abcissa. Considere o sólido
truncado que apresenta a figura da secção visível em ambas as projeções.
Sem comentários:
Enviar um comentário