TESTE 2 DO 11AV2 - 2017/2018

Enunciado e proposta de resolução:

1.      Represente, pelas suas projeções, a reta p, perpendicular ao plano oblíquo α.

Dados

– o plano oblíquo α é definido pelos pontos A(5;–6;6), B(0;1,5;3) e C(–5;5;3);

– a reta p contém o ponto Q(–7;5;10).

  

2.      Represente pelas suas projeções o quadrado [ABCD], contido num plano oblíquo β.

Dados

– o ponto A(–5,5;5;3) é um dos vértices do quadrado;

– o vértice C tem 0 de abcissa e 2,5 de afastamento;

– a diagonal [AC] pertence a uma reta oblíqua passante p;

– o traço horizontal do plano β faz, com o eixo x, um ângulo de 45⁰, com abertura para a direita.

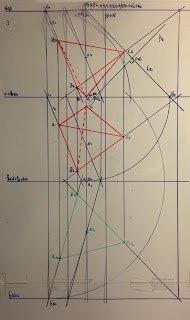
3.      Represente, pelas suas projeções, uma pirâmide regular de base triangular [ABC] situada num plano de rampa ω.

Identifique, a traço interrompido, as arestas invisíveis do sólido.

Dados

–  A(5;3;6) é um vértice da base;

– o traço horizontal do plano ω tem 9 de afastamento;

– o vértice B tem 3 de abcissa e 8 de afastamento;

– o vértice C tem abcissa negativa;

– o vértice V do sólido pertence ao Plano Horizontal de Projeção.

4.      Determine, graficamente, a amplitude do ângulo formado pelas retas r e s.

Dados

– a reta r é paralela ao plano bissetor dos diedros pares (β_2,4);

– a projeção frontal da reta r faz um ângulo de 30⁰, de abertura para a esquerda, com o eixo x;

– o ponto F, traço frontal da reta r, tem 8 de abcissa e 8 de cota;

– a reta s é concorrente com a reta r no ponto P, com 3 de cota;

– as projeções da reta s são perpendiculares às projeções homónimas da reta r.