GD A 11: EXAME DA 1ª FASE DE 2019

ENUNCIADO E PROPOSTA DE RESOLUÇÃO:

1. Determine as projeções do ponto I, resultante da intersecção da reta f com o plano α.

Dados:

– o plano α é definido pelo ponto R (8; 0; 6) e pela reta horizontal h;

– a reta h contém o ponto S (2; 2; 3) e define um ângulo de 50º, de abertura para a direita, com o Plano Frontal de Projeção;

– a reta f é frontal e contém o ponto M (0; 7; –7);

– a projeção frontal da reta f é perpendicular ao traço frontal do plano α.

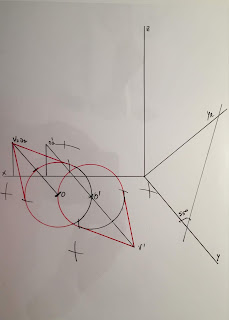
2. Determine as projeções de um hexágono regular [ABCDEF], pertencente a um plano oblíquo θ.

Dados:

– o plano θ é definido pelo ponto T, do eixo x, com 4 de abcissa, e pela reta de maior declive d;

– a reta d contém o ponto O (– 4; 4; 4) e a sua projeção horizontal define um ângulo de 50º, de abertura para a esquerda, com o eixo x;

– o ponto O é o centro do hexágono e o vértice A, de cota nula, pertence à reta d.

3. Represente, pelas suas projeções, o sólido resultante da secção produzida por um plano vertical δ num cubo.

Destaque, a traço mais forte, a parte do sólido delimitada pelo plano secante e pelo Plano Frontal de Projeção.

Preencha, com tracejado paralelo ao eixo x, a projeção visível da secção.

Dados:

– a face [ABCD] do cubo pertence a um plano de perfil com zero de abcissa;

– o vértice A tem 5 de cota e pertence ao Plano Frontal de Projeção;

– o lado [AB] define um ângulo de 50º com o Plano Horizontal de Projeção e o vértice B tem cota nula;

– a outra face de perfil tem abcissa negativa;

– o plano δ define um diedro de 30º, de abertura para a esquerda, com o Plano Frontal de Projeção e contém o vértice de maior cota da face de perfil com abcissa zero.

4. Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por dois cones

de revolução.

Destaque, no desenho final, apenas as linhas visíveis do sólido resultante.

Dados:

Sistema axonométrico:

– a projeção axonométrica do eixo y faz um ângulo de 130º com a projeção axonométrica do eixo x e um ângulo de 140º com a projeção axonométrica do eixo z;

– a inclinação das retas projetantes com o plano axonométrico é de 55º.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.

Cones:

– os cones são iguais e têm bases paralelas ao plano coordenado xz.

Cone 1:

– o ponto O (12; 9; 3) é o centro da circunferência da base tangente ao plano coordenado xy;

– o vértice V pertence ao plano coordenado xz.

Cone 2:

– o ponto O’ (9; 9; 3) é o centro da base;

– o vértice V’ tem maior afastamento do que a base.