TESTE SUMATIVO Nº 1 - 11AV2 - 2016/2017

 ENUNCIADO E PROPOSTA DE RESOLUÇÃO:

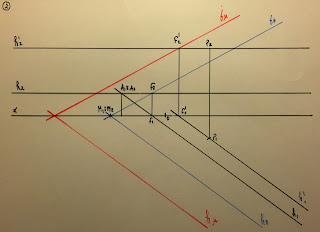
1.       Determine as projeções do plano de rampa θ ortogonal ao plano α.

Dados

– o plano α contém o ponto A(3;3;4) e a reta r;

– a reta r contém os pontos R(0;5;–5) e S(–4;–4;4);

– o plano de rampa θ contém o ponto A.

  

2.       Determine os traços do plano μ paralelo ao plano θ.

Dados

– o plano θ contém a reta h e o ponto M(5;0;0);

– a reta h é horizontal e contém o ponto A pertencente ao bissetor dos diedros pares, β_2,4, com 4 de abcissa e 2 de cota;

– a projeção horizontal da reta h faz um ângulo de 35⁰, de abertura para a direita, com o eixo x;

– o plano μ contém o ponto P(–4;2;6).

3.      Represente o retângulo [ABCD], situado no 1º diedro.

Dados

– o retângulo está contido num plano oblíquo α;

– os traços, horizontal e frontal, do plano α fazem, respetivamente, ângulos de 40⁰ (a.e.) e 60⁰ (a.d.) com o eixo x e são concorrentes num ponto de abcissa nula;

– o vértice A do retângulo tem abcissa nula e 3 de cota;

– o vértice B, consecutivo de A, pertence ao traço horizontal do plano α, e tem 2,5 de   afastamento;

– o lado [AD] da figura mede 6 cm.

4.      Represente o hexágono regular [ABCDEF], situado no 1º diedro.

Dados

– o hexágono está contido num plano de rampa ρ;

– o traço horizontal do plano ρ tem 4 de afastamento;

– os pontos A(3;0;6) e D, com 3 de abcissa e 1 de cota, são extremos de uma diagonal maior do hexágono.

https://www.facebook.com/GeometriaDescritivaA/