ORTOGONALIDADE ENTRE DUAS RETAS OBRLÍQUAS

Represente, pelas suas projeções, uma reta p ortogonal à reta r.

Dados

– a reta r está definida pelos pontos A(–3;1; –2) e B(2;5;4);

– a reta p passa no ponto P(–1;2;3) e a sua projeção horizontal faz um ângulo de 60⁰ (a.e.).

Proposta de resolução:

Breves passos de resolução:

* Representa-se a reta r (a passar por A e B) de acordo com os dados fornecidos; 

* Representa-se o ponto P e por ele uma reta horizontal h ortogonal à reta r (poderia ter sido frontal);

* A reta horizontal h permite, a partir do seu traço frontal F, representar o plano pelos seus traços, que são perpendiculares às projeções da reta r no mesmo plano de projeção;

* Representa-se a projeção horizontal da reta p, a passar em P e com o ângulo 60⁰ (a.e.);

* Determinam-se os traços da reta p, que permitem determinar a sua projeção frontal. 

Note que a reta p pertence ao plano que é ortogonal à reta r pelo que p é ortogonal a r.

https://www.facebook.com/GeometriaDescritivaA/

INTERSEÇÃO DE DOIS PLANOS

Determine as projeções da reta de intersecção, i, dos planos oblíquos α e β, que contêm o mesmo ponto do eixo x.

Dados

– os traços do plano α intersectam o eixo x no ponto com –1 de abcissa e fazem, ambos, ângulos de 60⁰, de abertura para a direita, com esse mesmo eixo;

– o plano β é definido pelo seu traço horizontal e pela reta b;

– o traço horizontal faz um ângulo de 20⁰, de abertura para a direita, com o eixo x;

– a reta b é de perfil passante e contém o ponto B(2;6).

Breves passos de resolução:

* Representou-se o plano α pelos seus dados;

* Representou-se o traço horizontal do plano β e a reta b pelos seus dados. Note-se que a reta b é passante, pelo que também tem abcissa -1;

* Através da reta r horizontal (por opção, pois poderia ser frontal) determinou-se o traço frontal do plano β;

* Poder-se-ia determinar a reta i sem o traço frontal do plano β, mas esta não foi a opção;

* A reta i é passante, uma vez que os 2 planos contêm o mesmo ponto do eixo x, pelo que houve necessidade de determinar um segundo ponto da reta - o ponto I. Este ponto foi determinado através da determinação da interseção de 3 planos, uma vez que foi incluída a reta r num plano horizontal;

* Unido o ponto A do eixo x com o ponto I representou-se a reta i.


https://www.facebook.com/GeometriaDescritivaA/

QUESTÃO DE AULA 1 DE 2015/2016 - 11AV1/CT2

ENUNCIADO E PROPOSTA DE RESOLUÇÃO:

Determine os traços do plano μ paralelo ao plano θ.

Dados

– o plano θ contém a reta h e o ponto M(5;0;0);

– a reta h é horizontal e contém o ponto A pertencente ao bissetor dos diedros pares, β_2/4, com 4 de abcissa e 2 de cota;

– a projeção horizontal da reta h faz um ângulo de 35⁰, de abertura para a direita, com o eixo x;

– o plano μ contém o ponto P(–4;2;6).

https://www.facebook.com/GeometriaDescritivaA

PERPENDICULARIDADE E INTERSEÇÕES

Considere o plano oblíquo δ.
a) Determine as projeções da reta b perpendicular ao plano oblíquo δ.
b) Determine o ponto I de interseção da reta b com o plano oblíquo δ.

Dados
- O  plano δ contém o ponto A(3;5;-1); B(1;2;2); C(-4;-1;3).
- A reta b contém o ponto P(6;2;2).

Breves passos de resolução:

- Pelos três pontos (A, B e C) representaram-se duas retas paralelas (por opção).

- Determinaram-se os traços das duas retas, que permitiram determinar os traços do oblíquo δ.

- Pelo ponto P representou-se a reta b, cuja projeção frontal é ortogonal ao traço frontal do plano e cuja projeção horizontal é ortogonal ao traço horizontal do plano.

- Para determinar o ponto I, de interseção da reta b com o plano  oblíquo δ, recorreu-se ao "método geral de interseção de retas com planos (1. Incluir a reta b num plano projetante; 2. Determinar a reta i de interseção dos dois planos; 3. Determinar o ponto de interseção da reta b com a reta i).

Nota: A preto surgem os passos relativos à determinação dos traços oblíquo δ e a vermelho os passos de determinação do ponto I.

EXAME DE GEOMETRIA DESCRITIVA A - 2ª FASE 2015

ENUNCIADO E PROPOSTA DE RESOLUÇÃO

1.    Determine os traços do plano α perpendicular ao plano de rampa δ.

Dados

– o plano δ é definido pelo seu traço horizontal com 6 de afastamento e pelo ponto A;

– o ponto A, com 6 de abcissa e 4 de cota, pertence ao plano bissetor dos diedros ímpares, β_1,3;

– o plano α contém o ponto P(0;9;8);

– o traço frontal do plano α forma um ângulo de 45⁰, de abertura para a esquerda, com o eixo x.

2.    Determine a amplitude do ângulo entre o Plano Frontal de Projeção e o plano oblíquo ω.

Dados

– o plano ω é definido pelo ponto A(–4;6;5) e por uma reta horizontal h;

– a reta h contém o ponto B (0;4;2) e forma um ângulo de 50⁰, de abertura para a direita, com o Plano Frontal de Projeção.

3.    Determine as projeções e a verdadeira grandeza da figura de secção produzida por um plano vertical θ, num cubo situado no 1.º diedro.

Destaque, a traço mais forte, as projeções do cubo e da figura de secção e a sua verdadeira grandeza.

Identifique, a traço interrompido, a aresta invisível do sólido.

Dados

– o cubo tem duas faces frontais;

– o ponto A(3;0;3) e o ponto C(7;0;10) são vértices de uma diagonal da face frontal [ABCD];

– o plano θ contém o ponto M do eixo x com –1 de abcissa e forma um diedro de 45⁰, de abertura para a esquerda, com o Plano Frontal de Projeção.

4.    Represente, em axonometria clinogonal militar, uma forma tridimensional composta por dois prismas regulares de bases triangulares.

Destaque, no desenho final, apenas as linhas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– a projeção do eixo z forma um ângulo de 130° com a projeção do eixo x e um ângulo de 140° com a projeção do eixo y;

– a inclinação das retas projetantes em relação ao plano axonométrico é de 50°.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.

Prismas:

– as bases de menor cota dos prismas pertencem ao plano coordenado xy;

Prisma 1:

– os vértices R(6;2;0) e S(6;8;0) são os de maior abcissa de uma das suas bases;

– o prisma tem 9 cm de altura.

Prisma 2:

– os vértices R e Q (6;6;0) são os de menor abcissa de uma das suas bases;

– o prisma tem 5 cm de altura.

EXAME DE GEOMETRIA DESCRITIVA A - 1ª FASE 2015

1.       Determine os traços do plano θ paralelo ao plano de rampa ω.

Dados

– o plano ω contém a reta de perfil p, definida pelos pontos A(3;3;6) e B com 9 de afastamento e –2 de cota;

– o plano θ contém o ponto P de abcissa nula e –5 de cota, pertencente ao Plano Frontal de Projeção.

2.       Determine a amplitude do ângulo entre as direções das retas a e b.

Dados

– a reta a contém o ponto P(2;6;3);

– as projeções horizontal e frontal da reta a formam ângulos de 60⁰, de abertura para a direita, com o eixo x;

– a reta b é horizontal, contém o ponto S (–6; 5; 2) e forma um ângulo de 60⁰, de abertura para a esquerda, com o Plano Frontal de Projeção.

3.       Determine as projeções de um prisma oblíquo de bases regulares frontais, situado no 1º diedro, e das suas sombras, própria e projetada nos planos de projeção.

Destaque, a traço mais forte, as projeções do prisma e as linhas visíveis da sombra projetada nos planos de projeção e, a traço interrompido, as arestas invisíveis do sólido e as linhas invisíveis da parte ocultada da sombra projetada.

Identifique as áreas visíveis das sombras, própria e projetada, preenchendo-as a tracejado ou com uma mancha de grafite clara e uniforme.

Nota – Se optar pelo tracejado, deverá fazê-lo com linhas paralelas ao eixo x, nas áreas de sombra própria, e com linhas perpendiculares às projeções da direção luminosa, nas áreas de sombra projetada.

Dados

– o ponto A(0;0;0) e o ponto B(–3;0;5) são vértices consecutivos do quadrado [ABCD] de uma das bases do prisma;

– as projeções horizontais e frontais das retas que contêm as arestas laterais do prisma formam ângulos de 55⁰ e 35⁰, ambos de abertura para a direita, com o eixo x;

– o prisma tem 3 cm de altura;

– a direção luminosa é a convencional.

4.       Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por dois cones de revolução.

Destaque, no desenho final, apenas as linhas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– a projeção do eixo y forma um ângulo de 120⁰ com a projeção do eixo z e um ângulo de 150⁰ com a projeção do eixo x;

– a inclinação das retas projetantes em relação ao plano axonométrico é de 55⁰.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.

Cones:

– os dois cones são iguais e têm uma geratriz comum;

– o ponto O(9;2;5) e o ponto O’(6;12;5) são os centros das bases de cada um dos cones;

– as bases são paralelas ao plano coordenado xz e têm 3 cm de raio.

EXAME 2015 - 1ª FASE - GEOMETRIA DESCRITIVA A

Caros "discípulos", desejo que sejam competentes e coloquem em prática os conhecimentos adquiridos, no exame de Geometria Descritiva A, a realizar em 25/06/2015. Espero que sejam felizes e me ofereçam uma alegria, pelo Vosso bom desempenho.

Boa sorte a todos!!!

TESTE SUMATIVO N 6 - 2014/2015

1.       Determine as projeções da reta i, resultante da intersecção entre os planos δ e α.

Dados

– o plano δ é definido pelo ponto A(–4;4;2) e pela reta g;

– a reta g é fronto-horizontal com 2 de afastamento e 4 de cota;

– o plano α contém o ponto K do eixo x com 5 de abcissa e o seu traço frontal faz um ângulo de 60⁰, de abertura para a esquerda, com este eixo;

– o plano α é oblíquo e perpendicular ao β_2,4, bissetor dos diedros pares.

2.       Determine, graficamente, a amplitude do ângulo formado pela reta oblíqua r e o plano de topo θ.

Dados

– a reta r é definida pelos pontos A(–4;2;5) e B(0;6;–1);

– o plano θ contém o ponto S do eixo x com 3 de abcissa e faz um diedro de 60⁰, de abertura para a esquerda, com o Plano Horizontal de Projeção.

3.       Represente, pelas suas projeções, o sólido resultante da secção produzida por um plano de topo θ num cone de revolução com base situada num plano horizontal.

Destaque, a traço mais forte, a parte do cone delimitada pelo plano secante e pelo Plano Horizontal de Projeção.

Preencha, a tracejado, a projeção visível da secção.

Dados

– o ponto O(0;6;8) é o centro da base que tem 4 cm de raio;

– o vértice V do sólido pertence ao Plano Horizontal de Projeção;

– o plano de topo θ contém o ponto M do eixo x com 2 de abcissa e é paralelo à geratriz mais à direita do sólido.

4. a       Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por dois cubos.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– a projeção axonométrica do eixo y faz um ângulo de 145⁰ com a projeção do eixo z e um ângulo de 125⁰ com a projeção do eixo x;

– a inclinação das retas projetantes com o plano axonométrico é de 55⁰.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.

Cubos:

– os dois cubos são iguais e têm 5 cm de aresta, ambos com faces paralelas aos planos coordenados;

– o ponto A(2;7;7) é o vértice de um dos cubos com menor abcissa, maior afastamento e maior cota;

      – o ponto M(12;7;0) é o vértice do outro cubo com maior abcissa, maior afastamento e menor cota.

4. b Represente, em axonometria clinogonal cavaleira, uma forma tridimensional composta por um prisma regular de base quadrangular e por um cubo.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– a projeção axonométrica do eixo y faz um ângulo de 135⁰ com as projeções dos eixos z e x;

– a inclinação das retas projetantes com o plano axonométrico é de 55⁰.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente, da direita para a esquerda.

Prisma quadrangular:

– as bases do prisma pertencem a planos frontais;

– o ponto A (4;12;0) e o ponto C (9;12;5) são os vértices de uma das diagonais da base de maior afastamento do prisma;

– o prisma tem 11 cm de altura.

Cubo:

– as faces do cubo são paralelas aos planos coordenados;

– o vértice C é comum aos dois sólidos, sendo o vértice de menor abcissa, maior afastamento e maior cota do cubo;

       – a aresta do cubo mede 3 cm.

QUESTÃO DE AULA 3 - 2014/2015

11º AV2

Construa uma representação axonométrica ortogonal de uma forma tridimensional composta por um

prisma quadrangular regular e por uma pirâmide triangular oblíqua de base regular, de acordo com os

dados abaixo apresentados.

Ponha em destaque, no desenho final, apenas o traçado das arestas visíveis do sólido resultante.

Dados

Sistema axonometrico:

– trimetria:

a projecção axonométrica do eixo y faz ângulos de 130⁰ e de 120⁰ com as projecções dos eixos x e z,

respetivamente.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x, orientado positivamente da direita para a esquerda.

Sólidos:

– os pontos R(5;5;11) e S(0;5;11) definem uma aresta comum.

Prisma quadrangular regular:

– uma base está situada no plano coordenado horizontal xy;

– os pontos R e S definem a aresta de maior afastamento da outra base.

Piramide triangular obliqua de base regular:

– a base [RST] é paralela ao plano coordenado horizontal xy, sendo T o ponto de maior afastamento;

– o vértice da pirâmide coincide com o centro da face de maior afastamento do prisma.

11º AV1/CT2

Represente, em axonometria ortogonal, uma forma tridimensional composta por dois prismas regulares.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido resultante.

Dados

Sistema axonométrico:

– dimetria: a projeção axonométrica do eixo z faz um ângulo de 125⁰ com as projeções dos eixos x e y.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x orientado positivamente, da direita para a esquerda.

Prisma hexagonal:

– as bases do prisma pertencem a planos horizontais;

– o ponto A(5;0;3) e o ponto B(10;0;3) são os vértices da aresta de menor afastamento de uma das bases do prisma;

– a outra base está situada no plano coordenado xy.

Prisma triangular:

– as bases do prisma pertencem a planos frontais;

– o segmento [AB] é a aresta de menor cota de uma das bases deste prisma;

– a outra base pertence ao plano que contém a face lateral de maior afastamento do prisma hexagonal.

PREPARAÇÃO DO TESTE N 6 E DO EXAME 2015

Para melhor preparação do teste n 6 e exame 2015 aqui ficam alguns links que podem ser interessantes.


http://bi.gave.min-edu.pt/exames/exames/eSecundario/754/?listProvas


http://www.aproged.pt/examesgeometria.html

TESTE SUMATIVO Nº 5 - ENUNCIADO E PROPOSTA DE RESOLUÇÃO

TESTE SUMATIVO Nº 5 - ENUNCIADO E PROPOSTA DE RESOLUÇÃO:

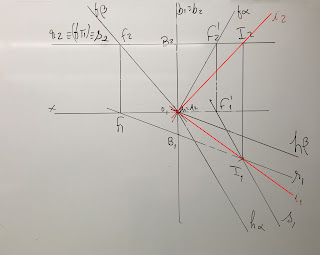
1.       Determine os traços do plano β, que contém os pontos P e R e é perpendicular ao plano α.

 Dados

Plano α:

– o plano α contém o ponto A (3; 6; 4) e uma reta horizontal h;

– a reta h tem 8 de cota, faz, com o plano frontal de projeção, um ângulo de 50⁰, com abertura para a direita, e o seu traço frontal F_h tem 6 de abcissa.

Plano β:

– o plano β contém os pontos P (0; 2; 4) e R (–5; 0; 0).

2.       Determine as projeções de um quadrado [ABCD], situado no 1º diedro e contido num plano oblíquo β.

Dados

– o lado [AB] está contido numa das retas de maior inclinação do plano oblíquo β;

– A(0;1,5;3) e B(–4;4,5;1).

3.       Determine a sombra própria e a sombra projetada nos planos de projeção de um cilindro oblíquo.

Destaque, a traço mais forte, as projeções do cilindro e o contorno da sua sombra projetada nos planos de projeção.

Identifique, a traço interrompido, as linhas invisíveis, quer no sólido, quer na parte ocultada do contorno da sua sombra projetada nos planos de projeção.

Identifique as áreas visíveis das sombras, própria e projetada, preenchendo-as a tracejado ou com uma mancha de grafite clara e uniforme.

Nota – Se optar pelo tracejado, deverá fazê-lo com linhas paralelas ao eixo x, nas áreas de sombra própria, e com linhas perpendiculares às projeções da direção luminosa, nas áreas de sombra projetada.

Dados

– as bases do cilindro são circunferências horizontais com 3 cm de raio;

– uma das bases está contida no plano horizontal de projeção, cujo centro é o ponto O (5;0) e a outra base tem 3 de cota;

– as geratrizes do contorno aparente, em projeção horizontal de frontal, fazem com o eixo x, respetivamente, ângulo de 60⁰ e 45⁰ de abertura para a direita;

– a direção luminosa é a convencional.

4. a)       Represente, em axonometria ortogonal, uma pirâmide quadrangular oblíqua, situada no 1º triedro.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido.

Dados

Sistema axonométrico:

– a projeção axonométrica do eixo z faz um ângulo de 110⁰ com a projeção do eixo x e um ângulo de 130⁰ com o eixo y.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x orientado positivamente, da direita para a esquerda.

Pirâmide quadrangular:

– os pontos A(3;0;0) e C(6;0;6)  são dois vértices opostos do quadrado;

– a aresta lateral [AV] é paralela ao eixo y;

– o vértice V da pirâmide tem 6 de afastamento.

4. b)    Represente, em axonometria ortogonal, uma pirâmide quadrangular oblíqua, situada no 1º triedro.

Destaque, no desenho final, apenas o traçado das arestas visíveis do sólido.

Dados

Sistema axonométrico:

– a projeção axonométrica do eixo z faz um ângulo de 110⁰ com a projeção do eixo x e um ângulo de 130⁰ com o eixo y.

Nota – Considere os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo x orientado positivamente, da direita para a esquerda.

Pirâmide quadrangular:

– os pontos A(3;0;0) e C(6;6;0)  são dois vértices opostos do quadrado;

– a aresta lateral [AV] é paralela ao eixo z;

– o vértice V da pirâmide tem 6 de cota.